- publication
- ACM Transactions on Graphics
- authors
- Michael Rabinovich, Roi Poranne, Daniele Panozzo, Olga Sorkine-Hornung
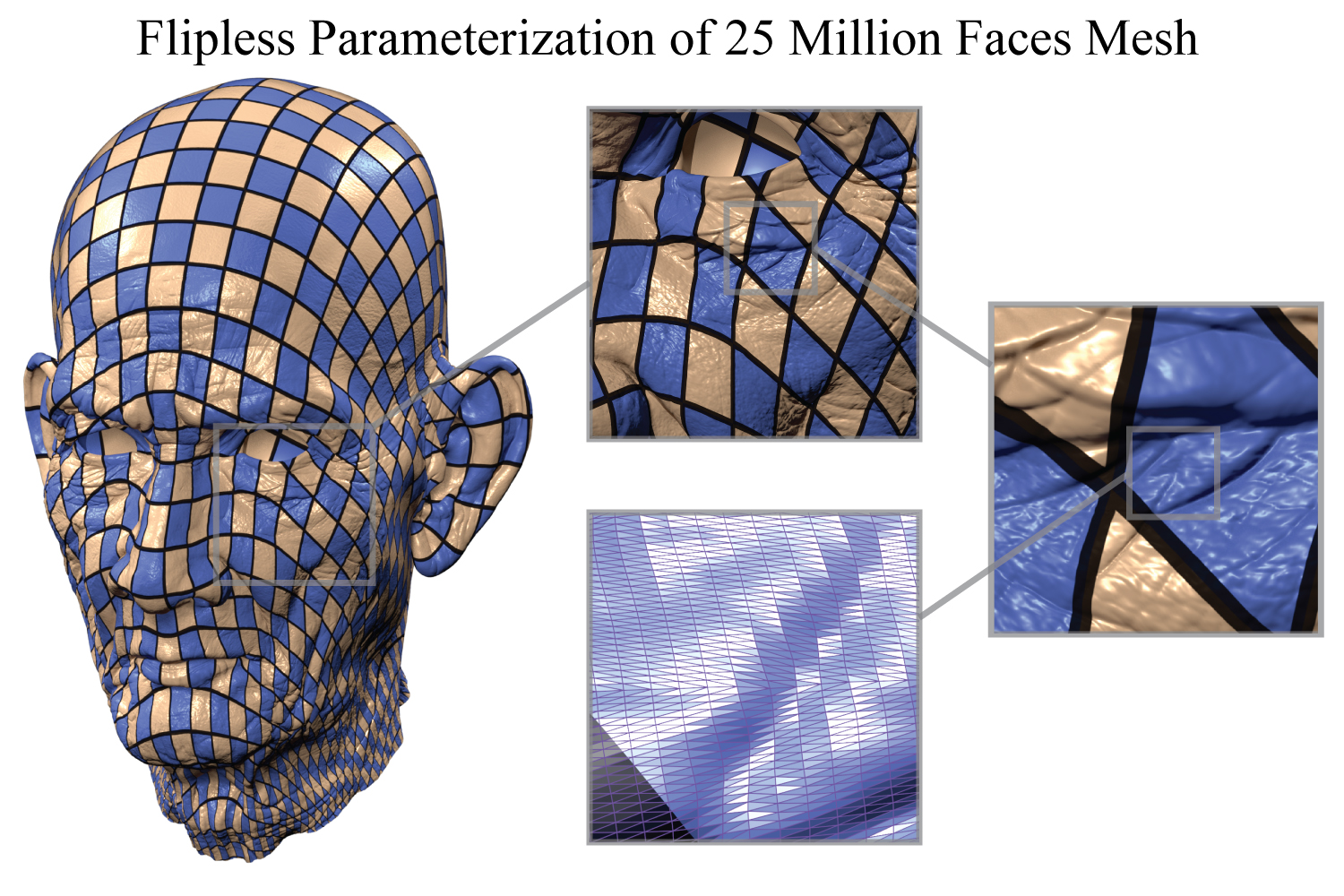
A locally injective parameterization obtained by minimizing the symmetric Dirichlet energy on a mesh with over 25 million triangles, computed with our algorithm in 80 minutes. The algorithm starts from a highly distorted locally injective initialization and in only 40 iterations, each requiring to solve a sparse linear system, it converges to a map with low isometric distortion that is guaranteed to be free of inverted elements.
abstract
We present a scalable approach for the optimization of flip-preventing energies in the general context of simplicial mappings, and specifically for mesh parameterization. Our iterative minimization is based the observation that many distortion energies can be optimized indirectly by minimizing a family of simpler proxy energies. Minimization of these proxies is a natural extension of the local/global minimization of the ARAP energy. Our algorithm is simple to implement and scales to datasets with millions of faces. We demonstrate our approach for the computation of maps that minimize a conformal or isometric distortion energy, both in two and three dimensions. In addition to mesh parameterization, we show that our algorithm can be applied to mesh deformation and mesh quality improvement.
downloads
- Paper (ACM Transactions on Graphics, official version available at dl.acm.org)
- Optimized parallel code on GitHub
- Reference implementation in libigl
- Results
- BibTex entry
accompanying video
acknowledgments
The authors would like to thank Shahar Kovalsky for providing the source code for AQP and for illuminating discussions, and the anonymous reviewers for their useful comments and suggestions. This work was supported in part by the ERC grant iModel (StG- 2012-306877), a gift from Adobe, and Courant Institute’s faculty start-up funding.