- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2013
- authors
- Christian Schüller, Ladislav Kavan, Daniele Panozzo, Olga Sorkine-Hornung
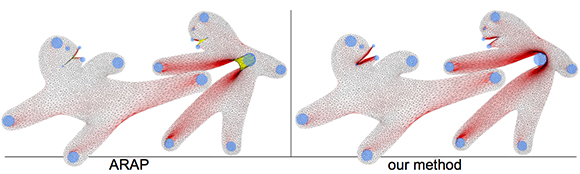
Popular deformation energies, such as As-Rigid-As-Possible, do not sufficiently penalize element inversion, and "spikes" and "spillages" might occur as a consequence (visualized in yellow). Our method modifies any given deformation energy, such that inversions are infinitely penalized. We derive an efficient numerical method to minimize the modified energy and produce a locally injective mapping of 2D and 3D domains.
abstract
Mappings and deformations are ubiquitous in geometry processing, shape modeling, and animation. Numerous deformation energies have been proposed to tackle problems like mesh parameterization and volumetric deformations. We present an algorithm that modifies any deformation energy to guarantee a locally injective mapping, i.e., without inverted elements. Our formulation can be used to compute continuous planar or volumetric piecewise-linear maps and it uses a barrier term to prevent inverted elements. Differently from previous methods, we carefully design both the barrier term and the associated numerical techniques to be able to provide immediate feedback to the user, enabling interactive manipulation of inversion-free mappings. Stress tests show that our method robustly handles extreme deformations where previous techniques converge very slowly or even fail. We demonstrate that enforcing local injectivity increases fidelity of the results in applications such as shape deformation and parameterization.
downloads
- Paper (SGP 2013, official version available at http://diglib.eg.org/)
- Paper (low resolution)
- Supplemental material
- Video
- Code
- BibTex entry
accompanying video
acknowledgments
We thank Kenshi Takayama for providing the binaries and source code of the Diffusion Surfaces modeling technique. We are also grateful to Yaron Lipman for sharing the MATLAB implementation of his Bounded Distortion method. This work was supported in part by the ERC grant iModel (StG-2012-306877).