- publication
- ACM SIGGRAPH 2005
- authors
- Yaron Lipman, Olga Sorkine-Hornung, Daniel Cohen-Or, David Levin
abstract
We introduce a rigid motion invariant mesh representation based on discrete forms defined on the mesh. The reconstruction of mesh geometry from this representation requires solving two linear systems that arise from the discrete forms: the first system defines the relationship between local frames on the mesh, and the second encodes the position of the vertices via the local frames. The reconstructed geometry is unique up to a rigid transformation of the mesh. We define surface editing operations by placing user-defined constraints on the local frames and the vertex positions. These constraints are incorporated in the two linear reconstruction systems, and their solution produces a deformed surface geometry that preserves the local differential properties in the least-squares sense. Linear combination of shapes that are expressed with our representation enables linear shape interpolation that correctly handles rotations. We demonstrate the effectiveness of the new representation with various detail-preserving editing operators and shape morphing.
downloads
- Paper (ACM SIGGRAPH 2005, official version available at http://portal.acm.org/)
- BibTex entry
- Video (shape interpolation)
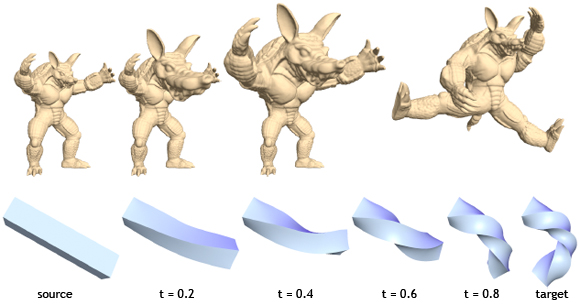
shape interpolation using our rotation-invariant coordinates
acknowledgments
We are grateful to Alon Lerner for helping with the video, to Kun Zhou for providing the Poisson Editing software, to Andrew Nealen for proofreading and to Gershon Elber and Leif Kobbelt for their valuable comments and suggestions. The Bunny and Armadillo are courtesy of of Stanford University, the Octopus is courtesy of Mark Pauly. This work was supported in part by grants from the Israel Science Foundation (founded by the Israel Academy of Sciences and Humanities) and the Israeli Ministry of Science.