- publication
- ACM SIGGRAPH 2011
- also in
- Communications of the ACM Research Highlights, April 2014
- authors
- Alec Jacobson, Ilya Baran, Jovan Popović, Olga Sorkine-Hornung

Bounded biharmonic blending supports points, bones, and cages arranged in an arbitrary configuration. This versatility makes it possible to choose the right tool for each subtask: bones to control rigid parts, cages to enlarge areas and exert precise control, and points to transform flexible parts. The weight computation is done at bind time so that high-quality deformations can be computed in real time with low CPU utilization.
abstract
Object deformation with linear blending dominates practical use as the fastest approach for transforming raster images, vector graphics, geometric models and animated characters. Unfortunately, linear blending schemes for skeletons or cages are not always easy to use because they may require manual weight painting or modeling closed polyhedral envelopes around objects. Our goal is to make the design and control of deformations simpler by allowing the user to work freely with the most convenient combination of handle types. We develop linear blending weights that produce smooth and intuitive deformations for points, bones and cages of arbitrary topology. Our weights, called bounded biharmonic weights, minimize the Laplacian energy subject to bound constraints. Doing so spreads the influences of the controls in a shape-aware and localized manner, even for objects with complex and concave boundaries. The variational weight optimization also makes it possible to customize the weights so that they preserve the shape of specified essential object features. We demonstrate successful use of our blending weights for real-time deformation of 2D and 3D shapes.
downloads
- Paper (ACM SIGGRAPH 2011, official version available at http://portal.acm.org/)
- Paper (low resolution)
- BibTex entry
- Video
- Supplemental video
- Fast-forward video
- 2D MATLAB demo
- 2d/3d demo binary (mac os x app), depends on and included in libigl
- Animato, a free iPad app based on this work
- biharmonic_bounded.m
- Tutorial
2D MATLAB demo (bbw_demo.m)

2D MATLAB demo (alligator_demo.m)

SIGGRAPH fast forward video (with sound)
accompanying video (with narration)
supplemental video (no audio)
follow-up technical report
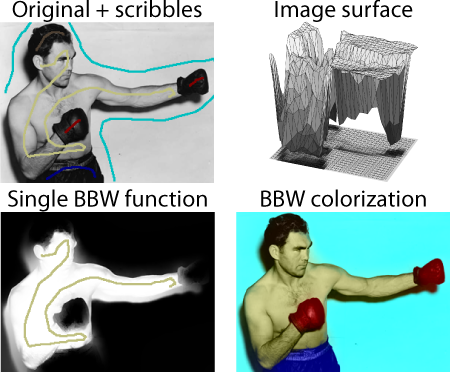
A Cotangent Laplacian for Images as Surfaces
by Alec Jacobson and Olga Sorkine, 2012 (BibTeX)
Abstract: By embedding images as surfaces in a high dimensional coordinate space defined by each
pixel’s Cartesian coordinates and color values, we directly define and employ cotangent-based, discrete
differential-geometry operators. These operators define discrete energies useful for image segmentation and
colorization.
acknowledgments
We are grateful to Jaakko Lehtinen, Bob Sumner and Denis Zorin for illuminating discussions and to Annie Ytterberg for her narration of the accompanying video. This work was supported in part by an NSF award IIS-0905502 and by a gift from Adobe Systems. Special thanks to Yang Song for his help implementing the rigidity brush and 2D remeshing. We also thank Scott Schaefer for providing the wooden gingerbread man image from "Image Deformation Using Moving Least Squares".