- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2014
- received
- Best Paper award
- authors
- Olga Diamanti, Amir Vaxman, Daniele Panozzo, Olga Sorkine-Hornung
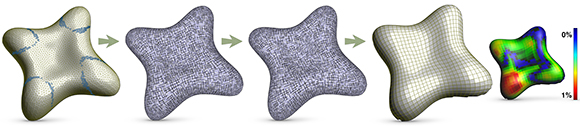
A smooth 4-PolyVector field is generated from a sparse set of principal direction constraints (faces in light blue). We optimize the field for conjugacy and use it to guide the generation of a planar-quad mesh. Pseudocolor represents planarity.
abstract
We introduce N-PolyVector fields, a generalization of N-RoSy fields for which the vectors are neither necessarily orthogonal nor rotationally symmetric. We formally define a novel representation for N-PolyVectors as the root sets of complex polynomials and analyze their topological and geometric properties. A smooth N-PolyVector field can be efficiently generated by solving a sparse linear system without integer variables. We exploit the flexibility of N-PolyVector fields to design conjugate vector fields, offering an intuitive tool to generate planar quadrilateral meshes.
downloads
- Paper (SGP 2014, official version available at http://diglib.eg.org/)
- Code
- BibTex entry
acknowledgments
We thank Mirela Ben-Chen for her insightful comments, Helmut Pottmann and Johannes Wallner for their major support, and Evolute GmbH, Alec Jacobson, Takeo Igarashi and Yang Liu for providing the models for our experiments. This work was supported in part by the ERC Starting Grant iModel (StG-2012-306877), and by the FWF Lise-Meitner grant M1618-N25.