- publication
- ACM SIGGRAPH ASIA 2015
- received
- Outstanding Software Award at SGP 2020
- authors
- Wenzel Jakob, Marco Tarini, Daniele Panozzo, Olga Sorkine-Hornung
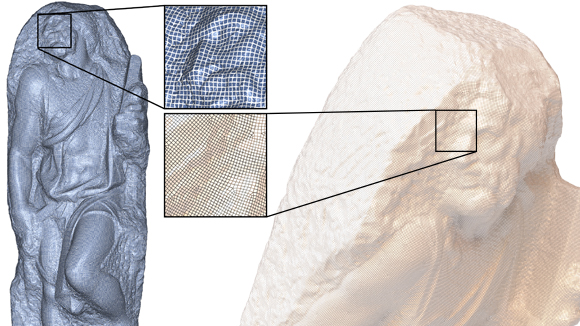
Our method scales to extremely large datasets, such as the 372M triangle St. Matthew statue acquired by the Digital Michelangelo project [Levoy et al. 2000]. The left side shows a visualization of the position field, and the right is the final quadrilateral mesh. The entire process takes 9 minutes and 18 seconds.
abstract
We present a novel approach to remesh a surface into an isotropic triangular or quad-dominant mesh using a unified local smoothing operator that optimizes both the edge orientations and vertex positions in the output mesh. Our algorithm produces meshes with high isotropy while naturally aligning and snapping edges to sharp features. The method is simple to implement and parallelize, and it can process a variety of input surface representations, such as point clouds, range scans and triangle meshes. Our full pipeline executes instantly (less than a second) on meshes with hundreds of thousands of faces, enabling new types of interactive workflows. Since our algorithm avoids any global optimization, and its key steps scale linearly with input size, we are able to process extremely large meshes and point clouds, with sizes exceeding several hundred million elements. To demonstrate the robustness and effectiveness of our method, we apply it to hundreds of models of varying complexity and provide our cross-platform reference implementation in the supplemental material.
downloads
- Paper (ACM SIGGRAPH ASIA 2015, official version available at http://portal.acm.org/)
- Paper (Low resolution)
- Data (All meshes used in comparisons; output from remeshing benchmark)
- Code and binaries (on GitHub)
- Video
- BibTex entry
accompanying video
acknowledgments
We thank Christian Schüller for 3D-scanning the meshes shown in Figures 1 and 20, Keenan Crane for helpful advice on visualizations of N-RoSy fields, and Olesya Jakob for designing the RoSy/PoSy illustrations shown in Figures 4 and 6. Emily Whiting provided voice narration for the video. This work was supported in part by the ERC Starting Grant iModel (StG-2012-306877) and the EU FP7 project ICT FET Harvest4D (http://www.harvest4d.org/, G.A. no. 323567). Wenzel Jakob was supported by an ETH/Marie Curie fellowship.