- publication
- ACM SIGGRAPH 2013
- authors
- Noa Fish, Melinos Averkiou, Oliver van Kaick, Olga Sorkine-Hornung, Daniel Cohen-Or, Niloy Mitra
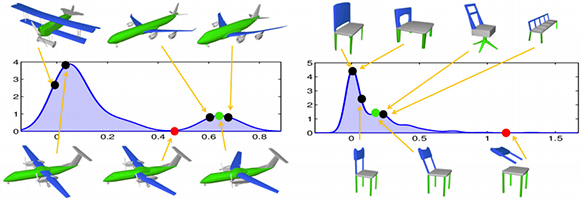
Meta-representations of two families of shapes, where we show one selected probability distribution from each representation. Here, we see the distribution for the angle between the main axes of airplane wings and fuselage, and the angle between the main axes of chair backs and legs. Note that the main axes are oriented to the same direction, implying that two orthogonal parts form a zero angle. There are two major modes in each distribution, where examples of shapes corresponding to the black dots are shown. Besides such exploration, the meta-representation can also be used for applications like guided editing: the user deforms selected shapes, taking them to lower probability states (red dots), and then the system, guided by the meta-representation, returns the shapes to higher probability states (green dots).
abstract
We introduce a meta-representation that represents the essence of a family of shapes. The meta-representation learns the configurations of shape parts that are common across the family, and encapsulates this knowledge with a system of geometric distributions that encode relative arrangements of parts. Thus, instead of predefined priors, what characterizes a shape family is directly learned from the set of input shapes. The meta-representation is constructed from a set of co-segmented shapes with known correspondence. It can then be used in several applications where we seek to preserve the identity of the shapes as members of the family. We demonstrate applica- tions of the meta-representation in exploration of shape repositories, where interesting shape configurations can be examined in the set; guided editing, where models can be edited while maintaining their familial traits; and coupled editing, where several shapes can be collectively deformed by directly manipulating the distributions in the meta-representation. We evaluate the efficacy of the proposed representation on a variety of shape collections.
downloads
- Paper (ACM SIGGRAPH 2014, official version available at http://portal.acm.org/)
- BibTex entry
- Video
accompanying video
acknowledgments
This work was supported in part by the Israeli Science Foundation (grant no. 1790/12), the U.S.-Israel Binational Science Foundation (grant no. 2012376), the Marie Curie Career Integration Grant 303541, the ERC Starting Grants iModel (StG-2012-306877) and SmartGeometry (StG-2013-335373), and gifts from Adobe Research. Oliver van Kaick is grateful to the Azrieli Foundation for the award of an Azrieli Fellowship. Melinos Averkiou is grateful to the Rabin Ezra Scholarship Trust for the award of a post-graduate bursary.