- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2012
- authors
- Alec Jacobson, Tino Weinkauf, Olga Sorkine-Hornung

Shape deformation: Recent works emphasize the importance of bounded control, but simply adding constant bounds to shape-aware smoothness energies of increasing order encourages more and more oscillation. Our framework efficiently optimizes such high-order energies as ∫M ‖∇ 4f ‖ while ensuring against spurious local extrema.
abstract
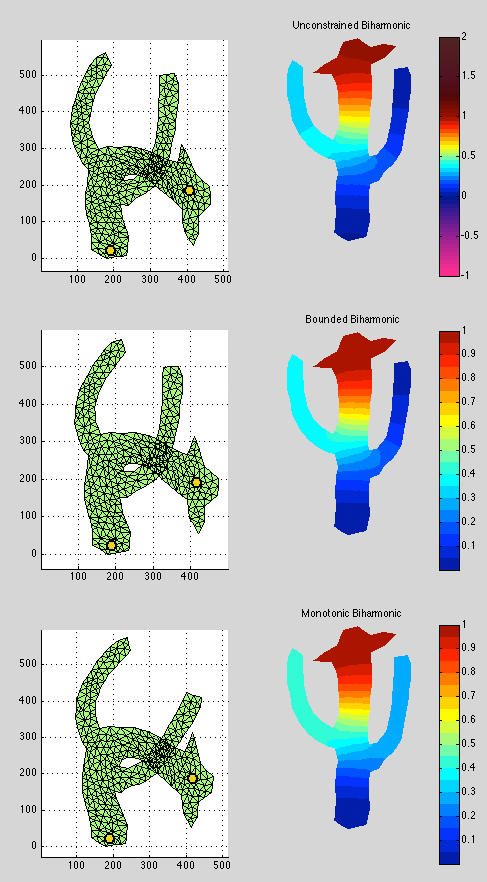
Functions that optimize Laplacian-based energies have become popular in geometry processing, e.g. for shape deformation, smoothing, multiscale kernel construction and interpolation. Minimizers of Dirichlet energies, or solutions of Laplace equations, are harmonic functions that enjoy the maximum principle, ensuring no spurious local extrema in the interior of the solved domain occur. However, these functions are only C0 at the constrained points, which often causes smoothness problems. For this reason, many applications optimize higher-order Laplacian energies such as biharmonic or triharmonic. Their minimizers exhibit increasing orders of continuity but also increasing oscillation, immediately releasing the maximum principle. In this work, we identify characteristic artifacts caused by spurious local extrema, and provide a framework for minimizing quadratic energies on manifolds while constraining the solution to obey the maximum principle in the solved region. Our framework allows the user to specify locations and values of desired local maxima and minima, while preventing any other local extrema. We demonstrate our method on the smoothness energies corresponding to popular polyharmonic functions and show its usefulness for fast handle-based shape deformation, controllable color diffusion, and topologically-constrained data smoothing.
downloads
- Paper (SGP 2012, official version available at http://diglib.eg.org/)
- Paper (low resolution)
- BibTex entry
- Video
- Matlab 2D Cactus Demo
- monotonic_biharmonic.m
accompanying video (with narration)
2D MATLAB cactus demo (cactus_demo.m)
acknowledgments
We thank Kenshi Takayama for his valuable feedback. This work was supported in part by an SNF award 200021_137879 and by a gift from Adobe Systems.