- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2013
- authors
- Leonardo Sacht, Alec Jacobson, Daniele Panozzo, Christian Schüller, Olga Sorkine-Hornung
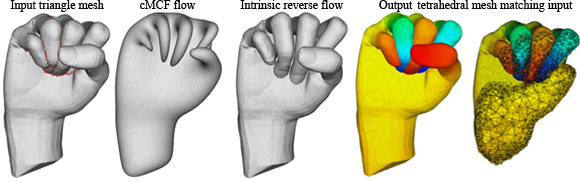
The triangle mesh of the Hand forms a closed surface, but contains nearly 2000 intersecting triangle pairs. Our method flows the surface according to conformalized mean-curvature flow (cMCF) until all self-intersections are removed. Then we reverse the flow so that shape intrinsics are restored but self-intersections are avoided. Finally we can tet-mesh inside this surface and map the mesh so that it matches the original surface. We may then solve PDEs, such as this biharmonic function.
abstract
Decades of research have culminated in a robust geometry processing pipeline for surfaces. Most steps in this pipeline, like deformation, smoothing, subdivision and decimation, may create self-intersections. Volumetric processing of solid shapes then becomes difficult, because obtaining a correct volumetric discretization is impossible: existing tet-meshing methods require watertight input. We propose an algorithm that produces a tetrahedral mesh that overlaps itself consistently with the self-intersections in the input surface. This enables volumetric processing on self-intersecting models. We leverage conformalized mean-curvature flow, which removes self-intersections, and define an intrinsically similar reverse flow, which prevents them. We tetrahedralize the resulting surface and map the mesh inside the original surface. We demonstrate the effectiveness of our method with applications to automatic skinning weight computation, physically based simulation and geodesic distance computation.
downloads
- Paper (SGP 2013, official version available at http://diglib.eg.org/)
- Paper (low resolution)
- Data (input and output meshes)
- untangle.m
- Video
- BibTex entry
accompanying video
acknowledgments
The authors thank Ladislav Kavan, Diego Nehab, Tino Weinkauf, Enrico Puppo and Yotam Gingold for helpful conversations. We are grateful to Hang Si for making the software Tetgen available and for email discussions, Marco Attene for making Meshfix open source and Pascal Frey and the University of Paris VI for releasing Medit into the public domain. Thanks to TOSCA and Aim@Shape projects for providing triangle meshes that were used as input. We also thank Kenshi Takayama for reviewing the submitted version of this work. This work was supported in part by the ERC grant iModel (StG-2012-306877), by an SNF award 200021_137879, an Intel Doctoral Fellowship and an FCS-Switzerland Scholarship ESKAS Nr. 2012.0617.