- publication
- ACM SIGGRAPH ASIA 2020
- authors
- Alexandra Ion, Michael Rabinovich, Philipp Herholz, Olga Sorkine-Hornung
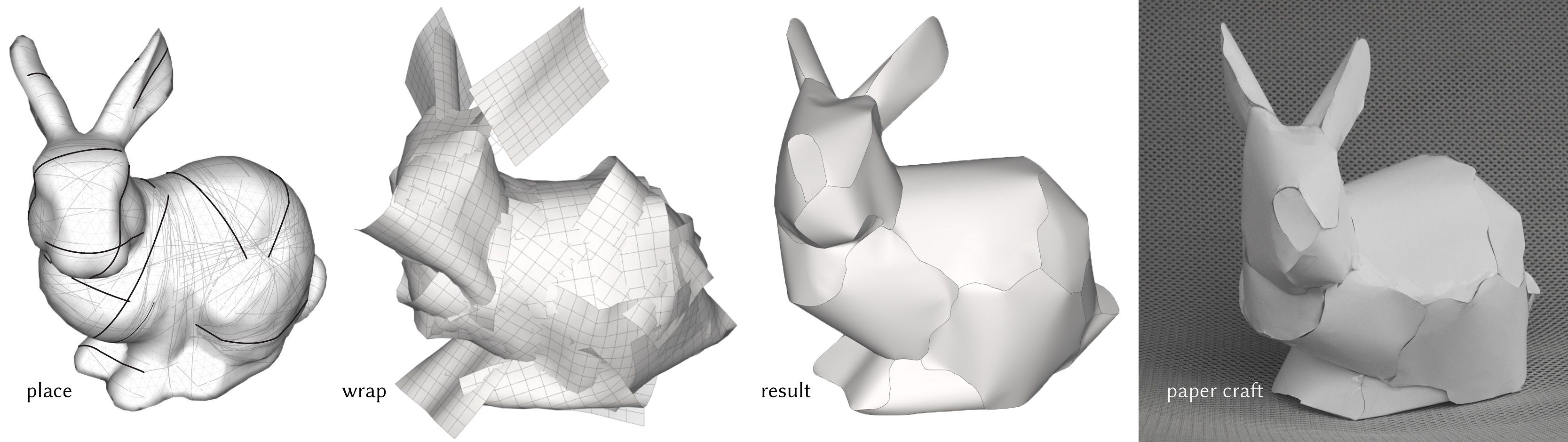
Our algorithm converts a given 3D shape into a piecewise developable surface that approximates it. We wrap the model in developable patches and nonlinearly project the original mesh onto the developables. This makes our algorithm mesh-independent and allows users to choose the approximation quality. Each patch in the end result can be fabricated using sheet material, e.g., paper.
abstract
We present an automatic tool to approximate curved geometries with piecewise developable surfaces. At the center of our work is an algorithm that wraps a given 3D input surface with multiple developable patches, each modeled as a discrete orthogonal geodesic net. Our algorithm features a global optimization routine for effectively finding the placement of the developable patches. After wrapping the mesh, we use these patches and a non-linear projection step to generate a surface that approximates the original input, but is also amendable to simple and efficient fabrication techniques thanks to being piecewise developable. Our algorithm allows users to steer the tradeoff between approximation power and the number of developable patches used. We demonstrate the effectiveness of our approach on a range of 3D shapes. Compared to previous approaches, our results exhibit a smaller or comparable error with fewer patches to fabricate.
downloads
videos
acknowledgments
We would like to thank David Lindlbauer for feedback, support and help with paper model fabrication and video production. This work was in part supported by the Swiss National Science Foundation (NCCR Digital Fabrication Agreement #51NF40-182887) and by a DAAD FIT fellowship.