- publication
- EUROGRAPHICS Symposium on Geometry Processing 2021
- authors
- Alexandre Binninger*, Floor Verhoeven*, Philipp Herholz, Olga Sorkine-Hornung *joint first authors
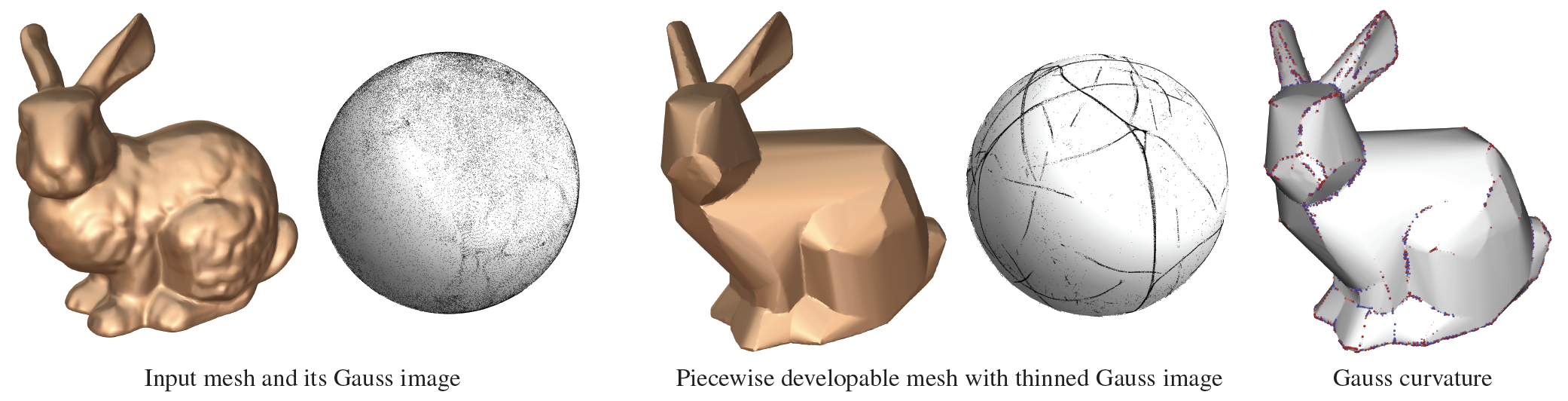
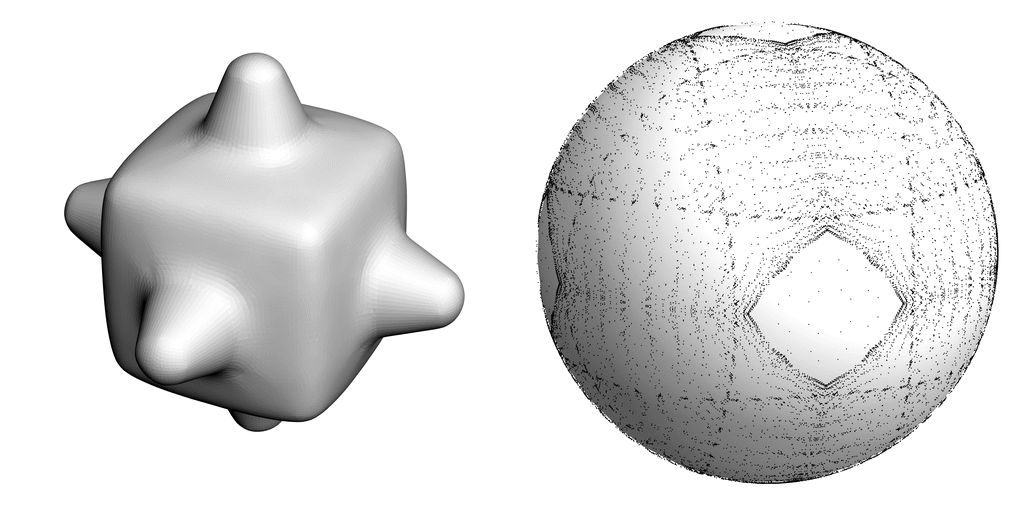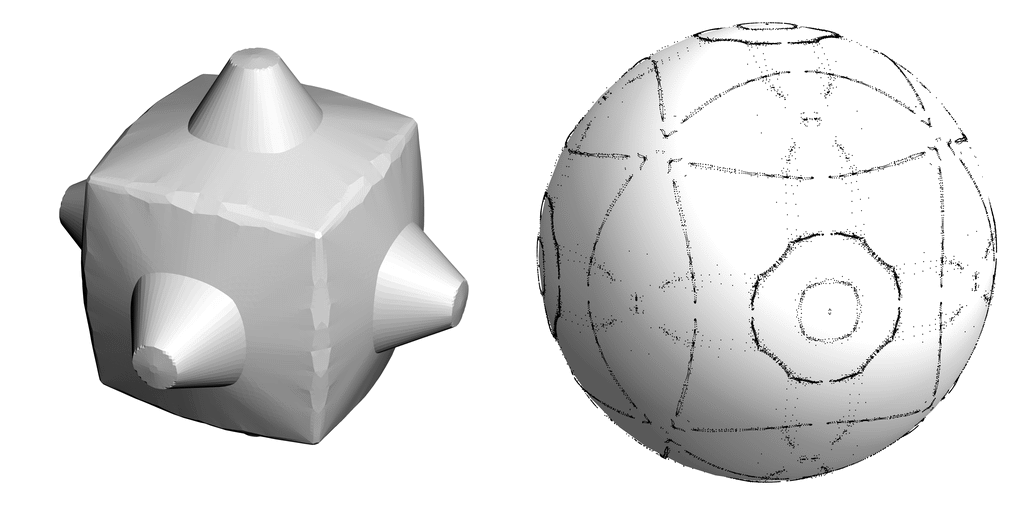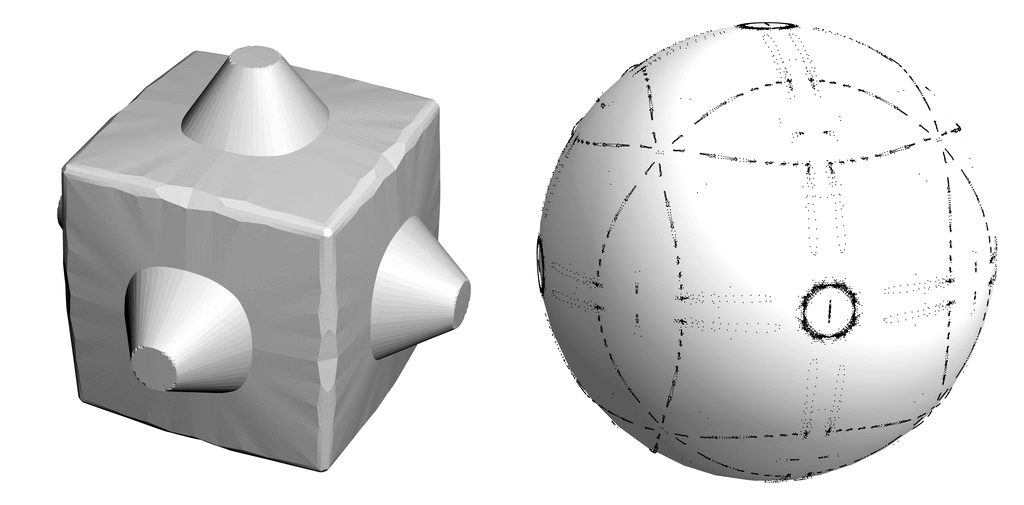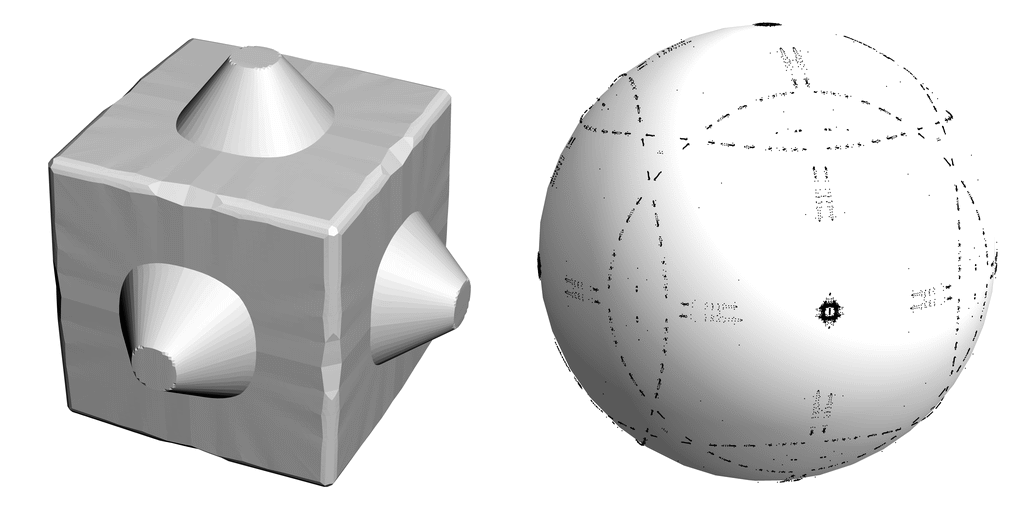
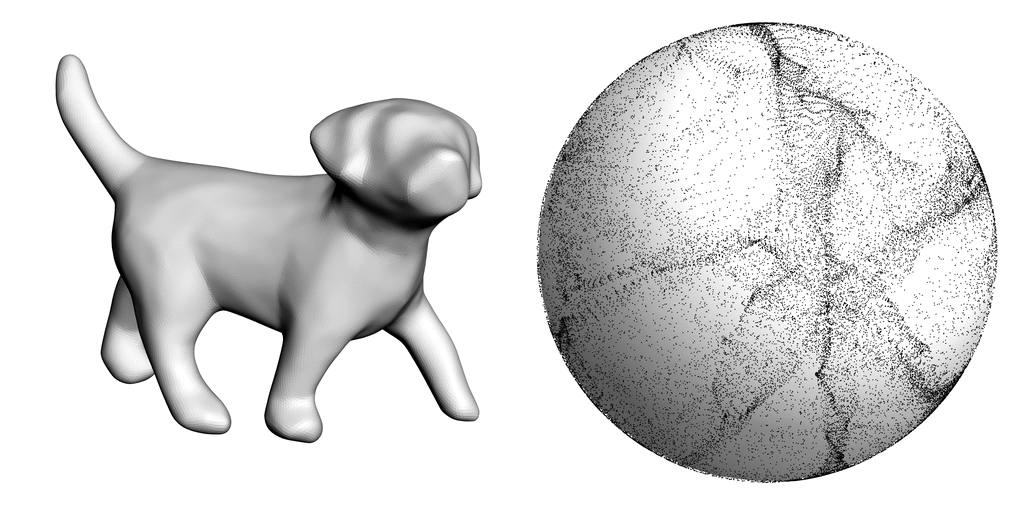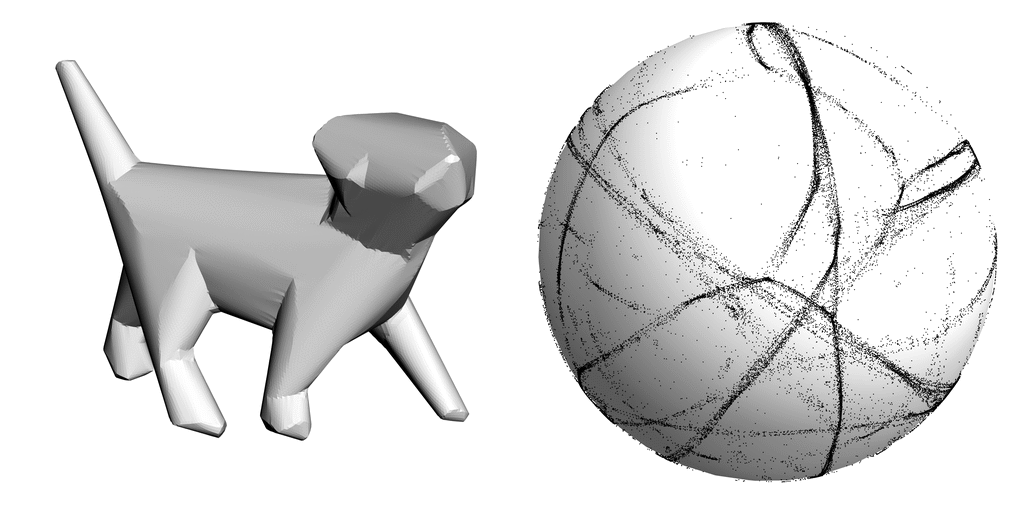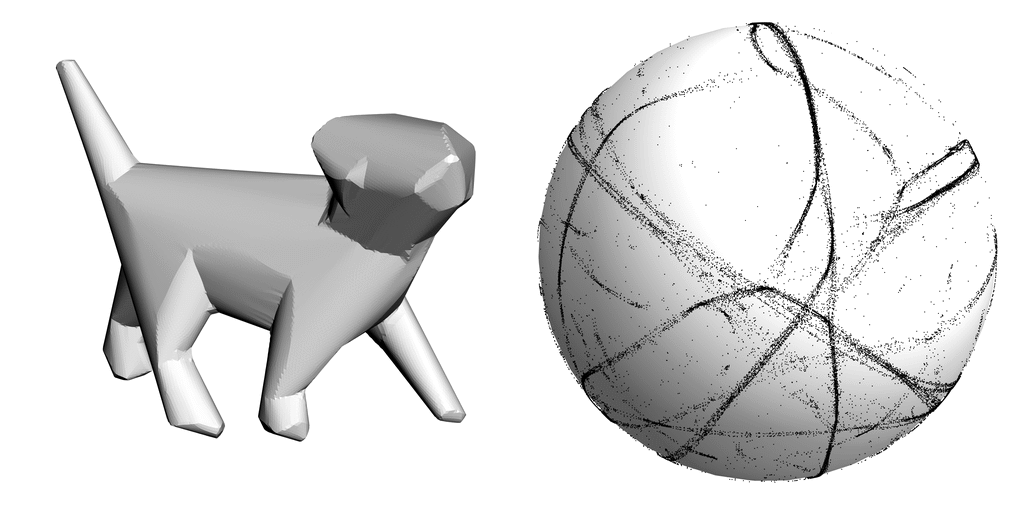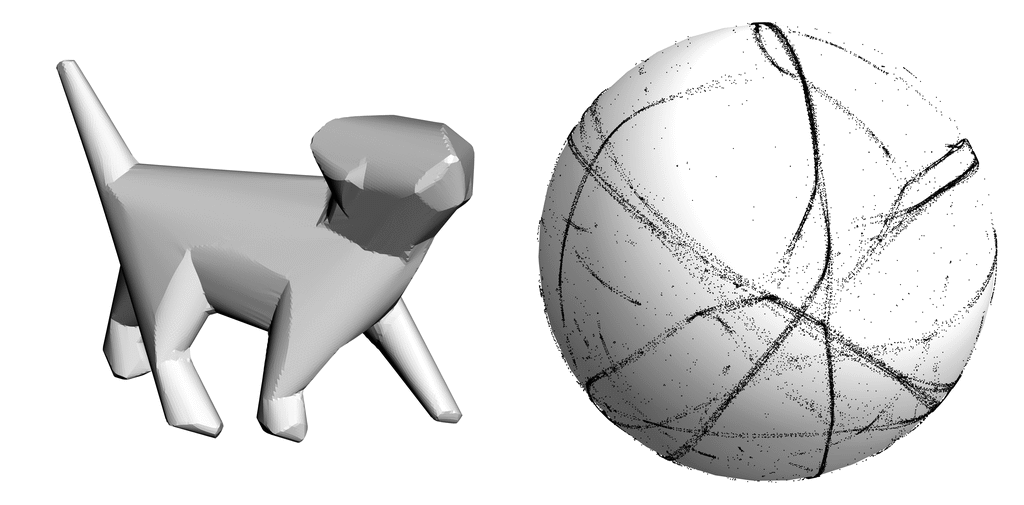
We present a method for approximating an input mesh with a piecewise developable surface by thinning its Gauss image. Using an iterative algorithm we are able to concentrate Gauss curvature on creases that naturally emerge over the course of the iterations.
abstract
Approximating 3D shapes with piecewise developable surfaces is an active research topic, driven by the benefits of developable geometry in fabrication. Piecewise developable surfaces are characterized by having a Gauss image that is a 1D object -- a collection of curves on the Gauss sphere. We present a method for developable approximation that makes use of this classic definition from differential geometry. Our algorithm is an iterative process that alternates between thinning the Gauss image of the surface and deforming the surface itself to make its normals comply with the Gauss image. The simple, local-global structure of our algorithm makes it easy to implement and optimize. We validate our method on developable shapes with added noise and demonstrate its effectiveness on a variety of non-developable inputs. Compared to the state of the art, our method is more general, tessellation independent, and preserves the input mesh connectivity.
animation


talk
downloads
acknowledgments
We thank the anonymous reviewers for their remarks. We also thank Amir Vaxman and Tim Hoffmann for the insightful discussions, which laid the foundation for this project. We are grateful to Silvia Sellán for providing us meshes for test and comparison purposes. This work was partially supported by the Personalized Health and Related Technologies (PHRT) SwissHeart grant and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No.101003104).