- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2014
- authors
- Kenshi Takayama, Daniele Panozzo, Olga Sorkine-Hornung
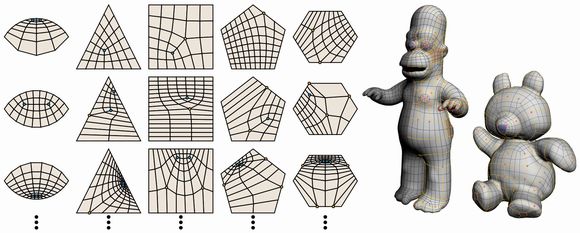
(Left) Quadrangulations of N-sided patches using our algorithm, where 2 ≤ N ≤ 6. Our algorithm is guaranteed to successfully quadrangulate N-sided patches with arbitrary numbers of edge subdivisions specified at the patch boundary. (Right) Integration of our algorithm into the sketch-based retopology system [Takayama et al. 2013].
abstract
We propose an algorithm to quadrangulate an N-sided patch (2 ≤ N ≤ 6) with prescribed numbers of edge subdivisions at its boundary. Our algorithm is guaranteed to succeed for arbitrary valid input, which is proved using a canonical simplification of the input and a small set of topological patterns that are sufficient for supporting all possible cases. Our algorithm produces solutions with minimal number of irregular vertices by default, but it also allows the user to choose other feasible solutions by solving a set of small integer linear programs. We demonstrate the effectiveness of our algorithm by integrating it into a sketch-based quad remeshing system. A reference C++ implementation of our algorithm is provided as a supplementary material.
downloads
- Paper (SGP 2014, official version available at http://diglib.eg.org/)
- Video
- Demo
- Slides
- BibTex entry
accompanying video
acknowledgments
The authors wish to thank Alexander Sorkine-Hornung and Maurizio Nitti for helpful discussion and feedback. The Bear model is courtesy of Takeo Igarashi. The Humanoid model is courtesy of the AIM@SHAPE Shape Repository. This work was supported in part by the ERC grant iModel (StG-2012-306877). Kenshi Takayama's stay at ETH Zurich until April 2014 was funded by JSPS Postdoctoral Fellowships for Research Abroad.