- publication
- ACM SIGGRAPH 2013
- authors
- Alec Jacobson, Ladislav Kavan, Olga Sorkine-Hornung
- award
- SIGGRAPH Test-of-Time Award 2024
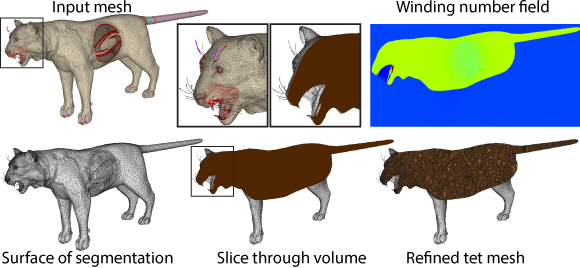
The Big SigCat input mesh has 3442 pairs of intersecting triangles (bright red), 1020 edges on open boundaries (dark red), 344 non-manifold edges (purple) and 67 connected components (randomly colored). On top of those problems, a SIGGRAPH logo shaped hole is carved from her side.
abstract
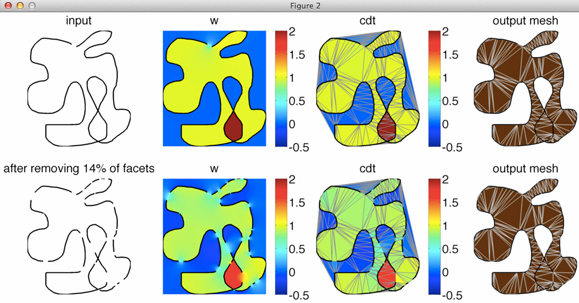
Solid shapes in computer graphics are often represented with boundary descriptions, e.g. triangle meshes, but animation, physically-based simulation, and geometry processing are more realistic and accurate when explicit volume representations are available. Tetrahedral meshes which exactly contain (interpolate) the input boundary description are desirable but difficult to construct for a large class of input meshes. Character meshes and CAD models are often composed of many connected components with numerous self-intersections, non-manifold pieces, and open boundaries, precluding existing meshing algorithms. We propose an automatic algorithm handling all of these issues, resulting in a compact discretization of the input’s inner volume. We only require reasonably consistent orientation of the input triangle mesh. By generalizing the winding number for arbitrary triangle meshes, we define a function that is a perfect segmentation for watertight input and is well-behaved otherwise. This function guides a graphcut segmentation of a constrained Delaunay tessellation (CDT), providing a minimal description that meets the boundary exactly and may be fed as input to existing tools to achieve element quality. We highlight our robustness on a number of examples and show applications of solving PDEs, volumetric texturing and elastic simulation.
downloads
- Paper (ACM SIGGRAPH 2013, official version available at http://portal.acm.org/)
- Paper (low resolution)
- Slides
- Slides (low resolution)
- Supplemental Images (high resolution)
- BibTex entry
- Video
- Data
- MATLAB (+mex) Demo
accompanying video
fast forward
supplemental images and data

.pdf with images
.zip of meshes
winding_demo_2d.m MATLAB Demo
winding_demo_3d.m MATLAB Demo

updates & hindsights
Since writing the paper we've received a lot of great feedback. A couple things have come to our attention.
The original publication had a typo in Equation (10), the
smoothness term for the graphcut. The otherwise term read
$1 / (2 sigma^2) a_{ij} * exp( | w(e_i) - w(e_j) |^2 )$.
It
should have been
$1 / (2 sigma^2) a_{ij} * exp(-| w(e_i) -
w(e_j) |^2 )$.
The correct version penalizes assigning different
labels to elements with similar winding number—as a smoothness
term should. This is what's happening in our code and what's in our
PDF now.
The citation and account of "Visibility-driven mesh analysis and visualization through graph cuts," by [Zhou, Zhang, Bittner and Wonka 2008] in our paper is misleading at best. We should have written something more like, "The method of [Zhou et al. 2008] uses ray-casting and graphcuts to assign inside/outside labels to each side of triangles in an unoriented input mesh. The resulting graphcut problem is potentially large and dense and requires extensive parameter tuning and heuristics when dealing with self-intersections and co-planar facets. Furthermore, fully or nearly enclosed cavity regions require user intervention." A comparison with this method would be very interesting, though admittedly it is solving a harder problem since their input is unoriented.
We write "This [naive evaluation of the winding number] is embarrassingly parallel and the geometric definition invites the possibility of a shader-style parallel implementation. However, the asymptotic runtime would still grow linearly with the number of input facets." While this true it doesn't tell the whole story: the GPU is very parallel and modern ones are quite fast. Martin Bisson has implemented the naive method on the GPU. According to some rough estimations, this will beat the pants off our divide-and-conquer heirarchical evaluation for input meshes smaller than 100,000 facets.
Rahul Narain has posted an alternative proof that the winding number is harmonic by reducing the continuous integral to a well known formula from electrostatics.
Ibraheem (ennetws) has wrapped our demo into a Autodesk 3ds Max script.
acknowledgments
We are indebted to Ilya Baran, Leo Guibas, Pierre Alliez, Alexander Sorkine-Hornung and Daniele Panozzo for illuminating conversations. We are grateful to Leonardo Koller Sacht, Fabian Hahn and Kaan Yücer for helping create results. Thanks to Josef Pelikan for recognizing the practical significance of winding numbers and including them in introductory computer graphics classes. Thanks to the Pascal Frey and the University of Paris VI for releasing the Medit software (used to visualize our 3D results) to the public domain. Also, thanks to Marco Attene for making his MeshFix program open source. This work was supported in part by the ERC grant iModel (StG-2012-306877), by an SNF award 200021_137879 and the Intel Doctoral Fellowship.