- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2003
- authors
- Olga Sorkine-Hornung, Daniel Cohen-Or, Sivan Toledo
- follow-up
- ACM Transactions on Graphics 24(4), 2005

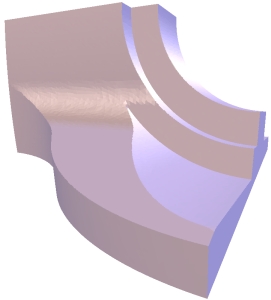
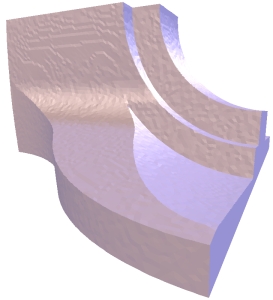
The delta-coordinates quantization to 5 bits/coordinate (left) introduces low-frequency errors to the geometry, whereas Cartesian coordinates quantization to 11 bits/coordinate (right) introduces noticeable high-frequency errors. The upper rows shows the quantized model and the bottom figures use color to visualize corresponding quantization errors.
abstract
Any quantization introduces errors. An important question is how to suppress their visual effect. In this paper we present a new quantization method for the geometry of 3D meshes, which enables aggressive quantization without significant loss of visual quality. Conventionally, quantization is applied directly to the 3-space coordinates. This form of quantization introduces high-frequency errors into the model. Since high-frequency errors modify the appearance of the surface, they are highly noticeable, and commonly, this form of quantization must be done conservatively to preserve the precision of the coordinates. Our method first multiplies the coordinates by the Laplacian matrix of the mesh and quantizes the transformed coordinates which we call "delta-coordinates". We show that the high-frequency quantization errors in the delta-coordinates are transformed into low-frequency errors when the quantized delta-coordinates are transformed back into standard Cartesian coordinates. These low-frequency errors in the model are much less noticeable than the high-frequency errors. We call our strategy high-pass quantization, to emphasize the fact that it tends to concentrate the quantization error at the low-frequency end of the spectrum. To allow some control over the shape and magnitude of the low-frequency quantization errors, we extend the Laplacian matrix by adding a number of spatial constraints. This enables us to tailor the quantization process to specific visual requirements, and to strongly quantize the delta-coordinates.applications.
downloads
- Paper (SGP 2003, official version available at http://diglib.eg.org/)
- BibTex entry (SGP 2003 paper)
- Talk slides from SGP 2003
- Follow-up analysis paper with Doron Chen. ACM Transactions on Graphics 24(4), 2005. Official version available at http://portal.acm.org/
- BibTex entry (ACM TOG paper)
low-frequency errors are less noticeable
The human perception seems to be more sensitive to normals/lighting errors.
Can you see a difference between these two horses?

|

|
|
original model |
delta-quantization (8 b/c, 1 anchor) |
There is a big difference in terms of geometric RMS error, but small "smoothness" or "normals" error.
some results
acknowledgments
We would like to thank Tali Irony for helping us with the implementation. The Max-Planck and Fandisk models are courtesy of Christian Roessl and Jens Vorsatz of Max-Planck-Institut fuer Informatik. This work was supported in part by grants from the Israel Science Foundation (founded by the Israel Academy of Sciences and Humanities), by the Israeli Ministry of Science, by an IBM Faculty Partnership Award, by the German Israel Foundation (GIF) and by the EU research project "Multiresolution in Geometric Modelling (MINGLE)" under grant HPRN-CT-1999-00117.