- publication
- Shape Modeling International 2004
- authors
- Olga Sorkine-Hornung, Daniel Cohen-Or
- follow-up
- IEEE Transactions on Visualization and Computer Graphics 11(2), 2005
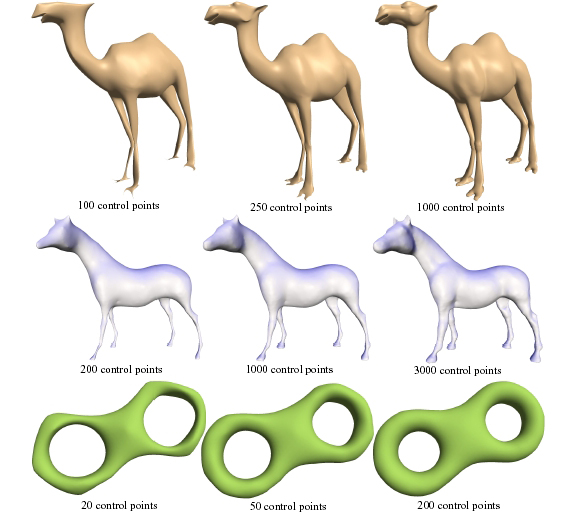
Examples of different LS-meshes. Each row displays LS-meshes computed using the same connectivity graph and a varying number of control points. Note that LS-meshes can have arbitrary topology, including genus greater than zero.
abstract
In this paper we introduce Least-squares Meshes: meshes with a prescribed connectivity that approximate a set of control points in a least-squares sense. The given mesh consists of a planar graph with arbitrary connectivity and a sparse set of control points with geometry. The geometry of the mesh is reconstructed by solving a sparse linear system. The linear system not only defines a surface that approximates the given control points, but it also distributes the vertices over the surface in a fair way. That is, each vertex lies as close as possible to the center of gravity of its immediate neighbors. The LS-meshes are a visually smooth and fair approximation of the given control points. We show that the connectivity of the mesh contains geometric information that affects the shape of the reconstructed surface. Finally, we discuss the applicability of LS-meshes to approximation of given surfaces, smooth completion and mesh editing.
downloads
- Paper (SMI 2004)
- BibTex entry (SMI 2004)
- Talk slides
- Follow-up paper "Geometry-Aware Bases for Shape Approximation", IEEE TVCG 11(2), 2005, with Dror Irony and Sivan Toledo.
- BibTex entry (IEEE TVCG paper)
acknowledgments
This work was supported in part by grants from the Israel Science Foundation (founded by the Israel Academy of Sciences and Humanities), by the Israeli Ministry of Science, by the German Israel Foundation (GIF) and by the EU research project ‘Multiresolution in Geometric Modelling (MINGLE)’ under grant HPRN-CT-1999-00117. The screwdriver mesh is courtesy of Cyberware.