- publication
- ACM SIGGRAPH 2014
- authors
- Daniele Panozzo, Enrico Puppo, Marco Tarini, Olga Sorkine-Hornung
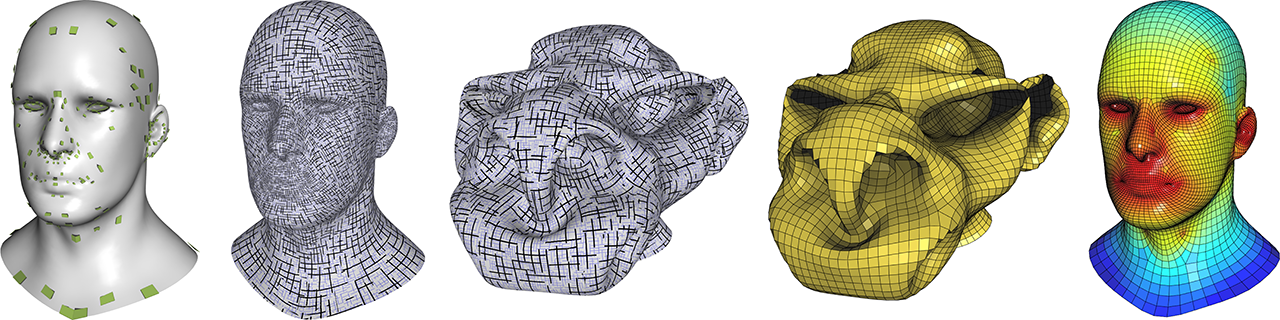
Given a sparse set of constraints defined on the input surface, we interpolate a dense, non-uniform, anisotropic and non-orthogonal frame field. We then deform the surface to warp this frame field into a cross field, which we use to guide a uniform, isotropic and orthogonal quadrangulation of the deformed surface. Finally, we deform the resulting quad mesh back onto the original surface and obtain a non-uniform, anisotropic and non-orthogonal quadrangulation that follows the prescribed frame field (color scale represents element areas).
abstract
We introduce frame fields, which are a non-orthogonal and non-unit-length generalization of cross fields. Frame fields represent smoothly varying linear transformations on tangent spaces of a surface. We propose an algorithm to create discrete, dense frame fields that satisfy a sparse set of constraints. By computing a surface deformation that warps a frame field into a cross field, we generalize existing quadrangulation algorithms to generate anisotropic and non-uniform quad meshes whose elements shapes match the frame field. With this, our framework enables users to control not only the alignment but also the density and anisotropy of the elements’ distribution, resulting in high-quality adaptive quad meshing.
downloads
- Paper (ACM SIGGRAPH 2014, official version available at http://portal.acm.org/)
- Supplemental material
- Video
- Source Code (libigl)
- Data
- BibTex entry
acknowledgments
The authors wish to thank: David Bommes for providing his Mixed-Integer solver; Nico Pietroni for his help in implementing the MIQ global parametrization; Hans-Christin Ebke for providing the code of the libQEx quadrangulator; Olga Diamanti for her ARAP implementation; Nikolas De Giorgis for the code to compute principal curvature directions; the repository of Aim@Shape, Alec Jacobson, Ladislav Kavan, Kenshi Takayama for providing datasets; Emily Whiting for narrating the accompanying video. This work was supported in part by the ERC Starting Grant iModel (StG-2012- 306877).