- publication
- EUROGRAPHICS/ACM SIGGRAPH Symposium on Geometry Processing 2010
- authors
- Alec Jacobson, Elif Tosun, Olga Sorkine-Hornung, Denis Zorin
abstract
Many problems in geometric modeling can be described using variational formulations that define the smoothness of the shape and its behavior w.r.t. the posed modeling constraints. For example, high-quality C² surfaces that obey boundary conditions on positions, tangents and curvatures can be conveniently defined as solutions of high-order geometric PDEs; the advantage of such a formulation is its conceptual representation-independence. In practice, solving high-order problems efficiently and accurately for surfaces approximated by meshes is notoriously difficult. Classical FEM approaches require high-order elements which are complex to construct and expensive to compute. Recent discrete geometric schemes are more efficient, but their convergence properties are hard to analyze, and they often lack a systematic way to impose boundary conditions. In this paper, we present an approach to discretizing common PDEs on meshes using mixed finite elements, where additional variables for the derivatives in the problem are introduced. Such formulations use first-order derivatives only, allowing a discretization with simple linear elements. Various boundary conditions can be naturally discretized in this setting. We formalize continuous region constraints, and show that these seamlessly fit into the mixed framework. We demonstrate mixed FEM in the context of diverse modeling tasks and analyze its effectiveness and convergence behavior.
downloads
- Paper (SGP 2010, official version available at http://diglib.eg.org/)
- Paper (low resolution)
- BibTex entry
- Slides from SGP July 2010 (without videos)
- Slides from SGP July 2010 (without videos, low resolution)
- Slides from Disney Tech Talk at ETH October 2010 (without videos)
- Slides from Disney Tech Talk at ETH October 2010 (without videos, low resolution)
- MATLAB codebase
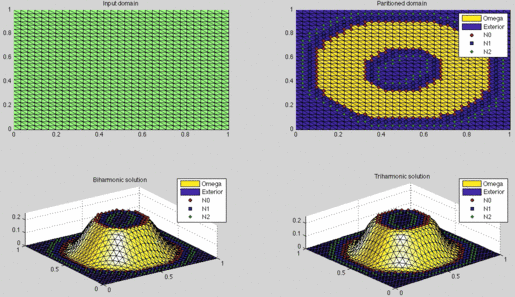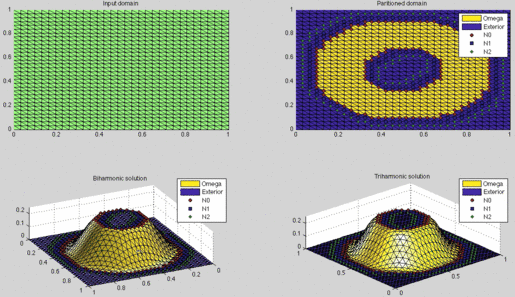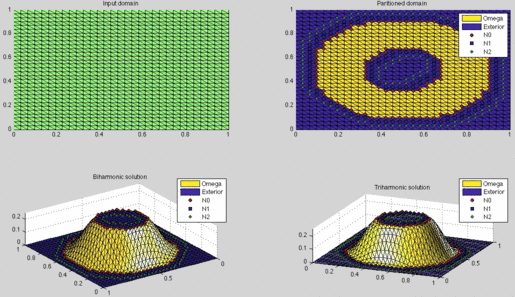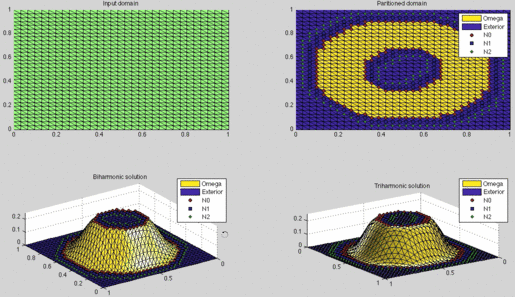
Screenshot of the bump_demo.m program included in the
MATLAB codebase.
screenshot videos
A half of a sphere is completed using the solution to the biharmonic equation to complete the hole. Tangent conditions are specified at a single point and interpolated around the boundary.
Max Planck's nose is exaggerated by specifying a new curvature of the surface along the bridge of his nose. Here we solve for the displacement of the points in the interior rather than their positions. This way detail is not lost.
Point boundary conditions may be used for interpolation control.
Curve boundary conditions expose tangent control for the biharmonic solution surface.
Curve conditions are well suited for drag and drop style manipulation.
screenshot GIFs

Region conditions are used to create a bump in a flat domain
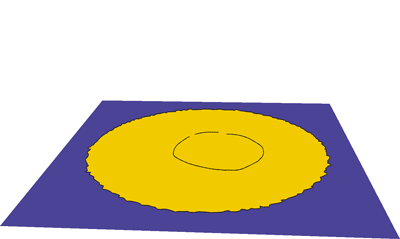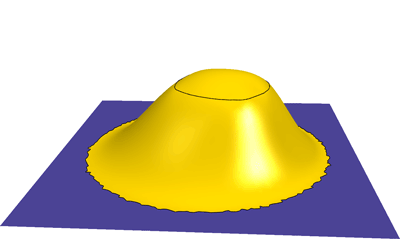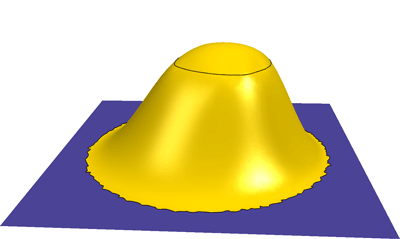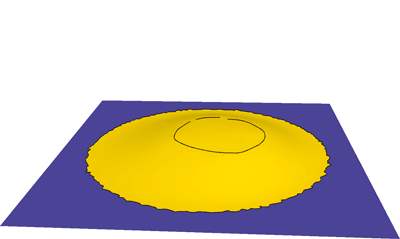
Curve conditions are used to create a bump in a flat domain

Point conditions are used to create a bumps in a flat domain
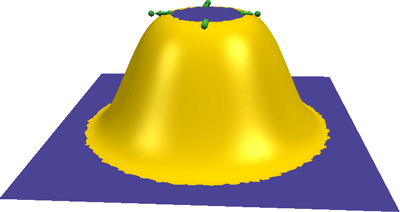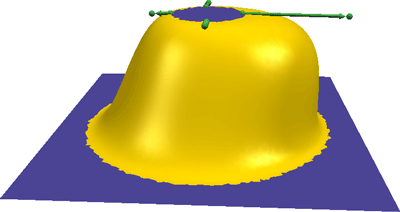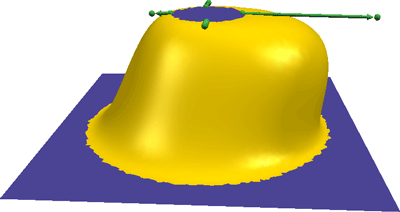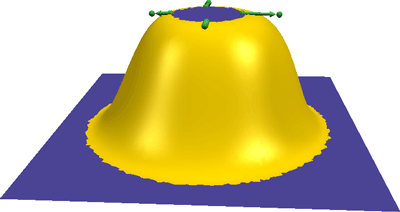
Tangent conditions are used to manipulate a bump.
acknowledgment
This work was supported in part by an NSF award IIS-0905502.
